إذا كان لنظام حل معادلتين خطيتين حلا واحد فقط يسمى نظام متسق ومستقل

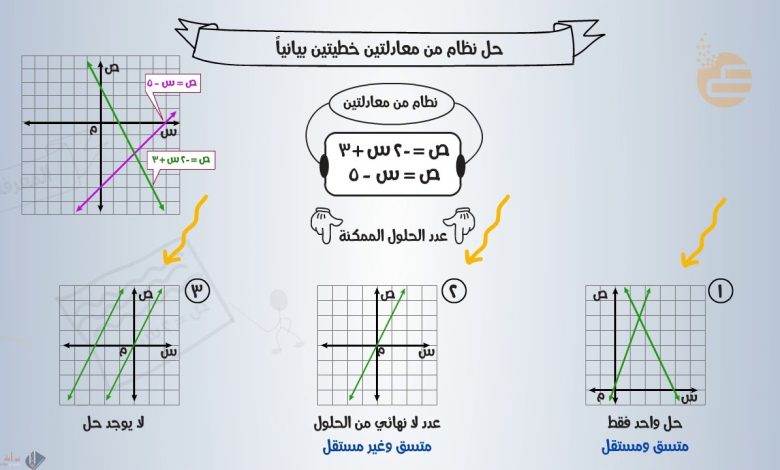
نظام المعادلات الخطية: بين الاستقرار والتنافر

في عالم الرياضيات، تحظى المعادلات الخطية بدور أساسي في حل الكثير من المشكلات الواقعية والنظرية. تقف المعادلات الخطية كأحد أهم أدوات الرياضيات التطبيقية، حيث تستخدم في حل العديد من المسائل في الفيزياء والهندسة والاقتصاد وغيرها من المجالات. ومن بين المفاهيم الأساسية التي تدور حولها المعادلات الخطية هي مفهوم النظام المتسق والمستقل.

النظام المتسق والمستقل:

عندما نتحدث عن نظام من المعادلات الخطية، نرمز إلى مجموعة من المعادلات التي تحتوي على مجموعة متنوعة من المتغيرات والثوابت. ويهمنا أن نعرف ما إذا كان هذا النظام قابلاً للحل وإن كان له حل وحيد أو عدة حلول أو لا يوجد حلا على الإطلاق.

عندما يكون لنظام المعادلات الخطية حل وحيد، فإننا نصفه بأنه “متسق ومستقل”. يعني ذلك أن الحل يمكن التوصل إليه بطرق معينة وواضحة، وأن قيم المتغيرات يمكن تحديدها بشكل دقيق.

أسباب الاستقرار:

تعتمد استقرارية النظام على تباين المعادلات المتواجدة فيه. عندما تحتوي المعادلات على معلومات متنافرة أو تعارضية، فإنها قد تفقد الاستقرارية، وبالتالي لا يمكن حلها بشكل مستقل.

التحقق من الاستقرارية:

يمكننا التحقق من استقرارية النظام عن طريق استخدام أساليب مثل طريقة التحليل الخطي وتطبيق قواعد الجبر الخطي. هذه الأساليب تساعد في فحص النظام وتحديد مدى قابليته للحل.

أهمية النظام المتسق والمستقل:

يكمن أهمية النظام المتسق والمستقل في قدرته على تقديم حلول واضحة ومحددة للمسائل الرياضية والواقعية. يتيح لنا هذا النوع من النظم فهماً أعمق للعلاقات الرياضية بين المتغيرات والثوابت في المسألة.تعتبر المعادلات الخطية ونظمها من الأساسيات في الرياضيات التطبيقية، وفهم الاستقرارية والمستقلية للنظم يسهم في تحليل العديد من المشكلات والتحديات في العديد من المجالات. لذا، يجب على الطلاب والباحثين والمهتمين بالرياضيات العمل على فهم هذه المفاهيم بشكل جيد، حيث تمثل أساسًا أساسيًا لحل المسائل الرياضية بدقة وفعالية.

بمجرد فهمنا لمفهوم النظام المتسق والمستقل، ندرك أنه ليس كل نظام معادلات خطية يكون متسقًا ومستقلاً. ففي بعض الحالات، قد يكون النظام غير متسق وغير مستقل، وهذا يعني عدم وجود حل لهذا النظام أو وجود عدد لا نهائي من الحلول أو أن الحل ليس واضحًا.

عندما يكون النظام غير متسق، يعني ذلك وجود تعارض أو تناقض بين المعادلات الموجودة في النظام، وبالتالي لا يمكن الوصول إلى حل. وعندما يكون النظام غير مستقل، يعني ذلك أن إحدى المعادلات يمكن تمثيلها كمجموعة من المعادلات الأخرى، مما يجعل النظام يحتوي على معلومات زائدة وغير ضرورية، وبالتالي يكون الحل غير واضح أو غير فعّال.

من المهم فهم النظام المتسق والمستقل لأنه يساعد في تحديد طرق حل المسائل الرياضية بشكل صحيح وفعّال. على سبيل المثال، في الهندسة، قد يكون لدينا نظام معادلات يمثل تفاعلًا في الأنظمة الديناميكية، ويجب أن يكون النظام متسقًا ومستقلًا لضمان استقرارية النظام وصحة الحلول.

في الختام، فإن فهم النظام المتسق والمستقل يعتبر جزءًا أساسيًا من دراسة الرياضيات وتطبيقاتها، ويمكن أن يساعد في حل مجموعة متنوعة من المشكلات الواقعية في مختلف المجالات. لذا، يجب علينا دائمًا التأكد من استقرارية النظام ومستقليته قبل البدء في حل المعادلات الخطية والاعتماد على النتائج التي نحصل عليها في التطبيقات العملية والعلمية.